Le théorème de Bayes

Rédigé et vérifié par le psychologue Sergio De Dios González

Écrit par Paula Villasante

Dernière mise à jour : 27 janvier, 2023

Le théorème de Bayes est l’un des piliers des probabilités. Il s’agit d’une théorie avancée par Thomas Bayes (1702-1761) au 18e siècle. Mais qu’est-ce que le scientifique a essayé d’expliquer exactement ?

Selon l’Académie royale espagnole, la probabilité exprime, dans un processus aléatoire, le rapport entre le nombre de cas favorables et le nombre de cas possibles. De nombreuses théories ont été développées autour des probabilités qui nous gouvernent aujourd’hui.

Lorsque nous allons chez le médecin, ce dernier nous prescrit ce qui a le plus de chances de nous convenir. Les publicitaires consacrent leurs campagnes aux personnes les plus susceptibles d’acheter le produit qu’ils veulent promouvoir. Nous choisissons l’itinéraire qui a le plus de chances de nous prendre le moins de temps.

L’une des lois de probabilité les plus célèbres est la loi de la probabilité totale. Pour la comprendre, prenons un exemple.

Disons que, dans un pays donné, 39 % de la population est constituée de femmes. Nous savons également que 22 % des femmes et 14 % des hommes sont au chômage. Alors, quelle est la probabilité (P) qu’une personne choisie au hasard dans la population active de ce pays soit au chômage ? Selon la théorie des probabilités, les données seraient exprimées comme suit :

• La probabilité que la personne soit une femme : P(F)
• La probabilité que la personne soit un homme : P(H)

Sachant que 39 % de la population est féminine, alors on en déduit que : P(F) = 0,39. Alors, nous comprenons : P(H) = 1 – 0,39 = 0,61. Le problème de l’argent nous donne également les probabilités conditionnelles :

• Probabilité qu’une personne soit au chômage, sachant qu’elle est une femme -> P (P|F) = 0,22.
• Probabilité qu’une personne soit au chômage, sachant qu’elle est un homme — P (P|H) = 0,14

En utilisant la loi de la probabilité totale, nous obtenons :

P (P) = P(F)P(P|F) + P(H)P(P|H)

P (P) = 0,22 × 0,39 + 0,14 × 0,61

P (P) = 0,17

Ainsi, la probabilité qu’une personne choisie au hasard soit au chômage est de 0,17. On constate que le résultat se situe entre les deux probabilités conditionnelles (0,22 < 0,17 < 0,14). De plus, elle est plus proche des hommes, car dans la population de ce pays inventé, ils sont majoritaires.

Le théorème de Bayes

Supposons maintenant qu’une personne adulte soit choisie au hasard pour remplir un formulaire et que l’on constate qu’elle n’a pas d’emploi. Dans ce cas, et compte tenu de l’exemple précédent, quelle est la probabilité que cette personne choisie au hasard soit une femme -P (F|P)- ?

Pour résoudre ce problème, nous allons appliquer le théorème de Bayes. Ce théorème est utilisé pour calculer la probabilité d’un événement en ayant des informations préalables sur cet événement.

Nous pouvons calculer la probabilité d’un événement A, sachant également que cet événement A possède une certaine caractéristique (B) qui conditionne sa probabilité. Dans ce cas, nous parlons de la probabilité que la personne choisie au hasard pour remplir un formulaire soit une femme.

Mais en plus, cette probabilité ne sera pas indépendante du fait que la personne sélectionnée soit au chômage ou non. Quelle est donc la formule de ce théorème *

La formule du théorème de Bayes

Comme tout autre théorème, pour calculer la probabilité, nous avons besoin d’une formule. La formule est définie comme suit :

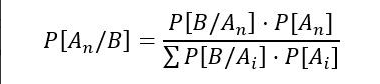
Cela semble compliqué, mais tout a une explication. Prenons les choses étape par étape. Que signifie chaque lettre ?

• Pour commencer, B est l’événement sur lequel nous disposons d’informations antérieures.
• En revanche, la lettre A(n) désigne les différents événements conditionnels.
• Dans la partie numérateur, nous avons la probabilité conditionnelle. Il s’agit de la probabilité que quelque chose (un événement A) se produise, sachant qu’un autre événement (B) se produit également. Elle est définie comme P(A|B) et s’exprime comme suit : La probabilité de A étant donné B.
• Au dénominateur, nous avons l’équivalent de P(B). Voir la section précédente.

Un exemple

Ainsi, pour revenir à l’exemple précédent, supposons qu’un adulte soit choisi au hasard pour remplir un questionnaire et que l’on observe qu’il est au chômage. Quelle sera la probabilité que cette personne choisie soit une femme ?

En tenant compte de l’exemple précédent, nous savons que 39 % de la population active sont des femmes. Nous savons donc que les autres sont des hommes. En outre, nous savons que le pourcentage de femmes au chômage est de 22 % et celui des hommes de 14 %.

Enfin, nous savons également que la probabilité qu’une personne choisie au hasard soit au chômage est de 0,17. Ensuite, si nous appliquons la formule du théorème de Bayes, le résultat que nous obtiendrons est qu’il y a une probabilité de 0,5 qu’une personne choisie au hasard, parmi toutes celles qui sont au chômage, soit une femme.

P(M|P) = (P(M) * P (P|M)/P(P)) = (0,22 * 0,39)/0,17 = 0,5

Concluons cet article sur les probabilités en faisant allusion à l’une des confusions les plus fréquentes en matière de probabilité. Celle-ci oscille entre 1 et 0, sans jamais sortir de ces marges ; 1 étant la probabilité d’un événement certain et 0 la probabilité d’un événement impossible.